Gimp Gih Matrix in Short - Part I
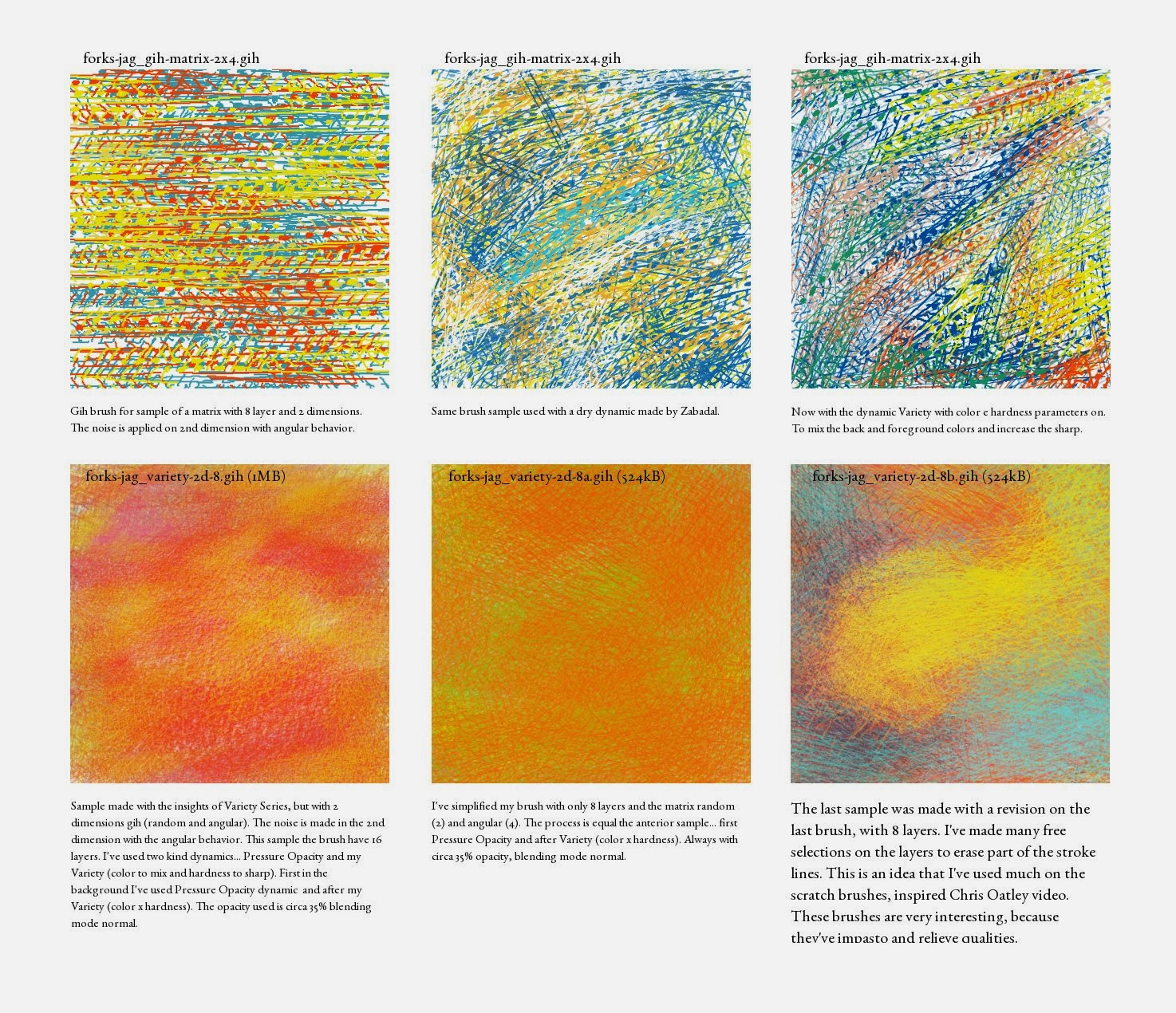 |
| Examples of my .gih sample matrix with 2 dimensions and the first brush series based in this tutorial. The brushes are thought of as bristle kind. |
Introduction
The more important thing to build dynamic brushes with more than one dimension is to imagine how they must work and the variations of the stains. To make dynamic brushes with many dimensions without this study, for me, doesn't make sense, for two things, mainly: first, is very difficult to control and organize the brushes by kind and second, the effect is very randomly. Normally, is better to simplify… all stains in a unique dimension with random behaviour.Dynamic raster gimp brush - the .gih matrix in short
To explain, in short, I prefer to use some examples with a matrix of two and three dimensions.
I imagined a matrix with 2 dimensions, the first dimension with 2 aspects (random) and 2nd dimension with 4 aspects (angular). To calculate the number of necessary layers on gimp we must multiply the ranks of two dimensions, 1st(2) x 2nd(4) = 8 layers.
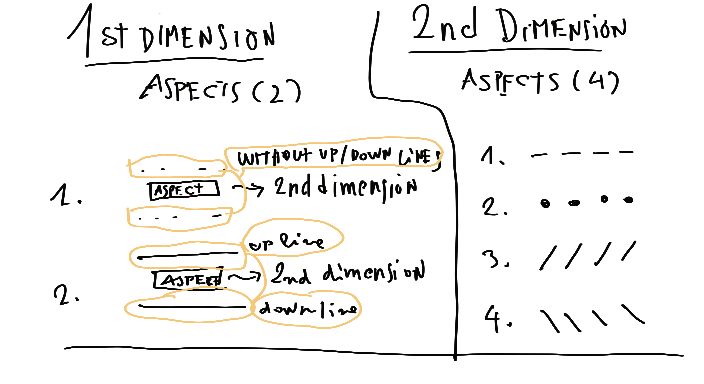
Is also useful to explain a bit more how we can transform the aspects in the correct order on the layer stack. When we talk about aspects… we are talking about the number of variations of these aspects that could have in a brushstroke. In many cases is useful to sketch on paper to imagine how it works before building it.
The 1st dimension is formed by 2 aspects random (without and with up-down lines), instead, the 2nd-second dimension has four aspects/variations, in my case, two dash lines types (hyphen and dots) and slash and backslash lines (/ and \).
The 2nd dimension is formed for 4 aspects (Angular = 0, 90, 180 and 270 degrees), each one is a different stain, in my case, I've made 4 images (one for each aspect):
- - - | Hyphen dash line => 0°
. . . | Point dash line) => 90°
/ / / | (slash kind line) => 180°
\ \ \ | Backslash kind line => 270°
To make the combination of these aspects in the stack layer on GIMP is a difficult task, then is interesting to make a sketch before.
My example is easier to imagine... the lines up and down (without and with) that can be together of 2nd dimension image aspects can be exemplified so:
The sequence of layers is ordered by dimensions and their aspects.
The first case - 2 dimensions .gih matrix
To understand better is interesting to imagine the aspects, as a possible change state of a pictorial stain. Normally thinking on digital painting issues, the aspects of the 2nd dimension modifies the aspect of the 1st dimension, in this sense could be understood as a subtle modifier of the aspects of 1st dimension, for example.I imagined a matrix with 2 dimensions, the first dimension with 2 aspects (random) and 2nd dimension with 4 aspects (angular). To calculate the number of necessary layers on gimp we must multiply the ranks of two dimensions, 1st(2) x 2nd(4) = 8 layers.
Is also useful to explain a bit more how we can transform the aspects in the correct order on the layer stack. When we talk about aspects… we are talking about the number of variations of these aspects that could have in a brushstroke. In many cases is useful to sketch on paper to imagine how it works before building it.
 |
| Box .gih matrix array metaphor. |

| Aspects of my .gih matrix sample. |
- - - | Hyphen dash line => 0°
. . . | Point dash line) => 90°
/ / / | (slash kind line) => 180°
\ \ \ | Backslash kind line => 270°
To make the combination of these aspects in the stack layer on GIMP is a difficult task, then is interesting to make a sketch before.
My example is easier to imagine... the lines up and down (without and with) that can be together of 2nd dimension image aspects can be exemplified so:
 |
| Organizing the stack layer on Gimp. |
The first aspect of 1st dimension
- 1st layer: 1st aspect of 2nd dim (hyphen dash lines) without lines up and down → 0°
- 2nd layer: 2nd aspect of 2nd dim (dot-dash lines) without lines up and down → 90°
- 3rd layer: 3rd aspect of 2nd dim (slash lines) without lines up and down → 180°
- 4th layer: 4th aspect of 2nd dim (backslash lines) without lines up and down → 270°
The second aspect of 1st dimension
- 5th layer: 1st aspect of 2nd dim (hyphen dash lines) with lines up and down → 0
- 6th layer: 2nd aspect of 2nd dim (dot-dash lines) with lines up and down → 90°
- 7th layer: 3rd aspect of 2nd dim (slash lines) with lines up and down →180°
- 8th layer: 4th aspect of 2nd dim (backslash lines) with lines up and down → 270
We need to organize the layer by groups, those of the 1st dimension and 2nd dimension. Explained in another way the general rule is:
Groups of 1st dimension = Total layers / 1st dimension aspects = Layers per group.
Will be 8/2=4 => that we have 2 groups with 4 layers (the are the aspects of 2nd dimension combined with 1st dimension).
Each group of 1st dimension is divided by the number of aspects of the 2nd dimension, in this case, 4/4=1, then we have one layer for each angular position, in total 4.
How it works
The first dimension is Random, so the aspects of the 2nd dimension will be printed randomly, without or with the lines up-down, in all aspects of the 2nd dimension:
- - - | . . . | / / / | \ \ \
The 2nd dimension is Angular and the aspects are printed following the angular variation of the stylus… in my .gih matrix example, this behaviour has only 4 states => 0, 90, 180 and 270°. Then the aspects:
- - - correspond to 0°;
The 2nd dimension is Angular and the aspects are printed following the angular variation of the stylus… in my .gih matrix example, this behaviour has only 4 states => 0, 90, 180 and 270°. Then the aspects:
- - - correspond to 0°;
. . . to 90°;
\ \ \ to 180° and,
/ / / to 270°
The .gih array for angular behaviour on gimp begins always with the 90° layer, in my example are the 2nd and 6th layers of the stack.
The array isn’t very precise with a short number of ranks to angular in the 2nd dimension but is sufficient to print correctly the major part of the stain aspects.
 |
| Sample of tests with .gih matrix brush. |
 |
| Angular precision of angular .gih with more steps. |
This sample was made with 8 layers… with 45° steps, is possible to see that the angular behaviour precision depends on the number of layers.
The brush is not created to drawing or painting… only to make a practical example of 2 dimensions gih matrix, but I’ve made a sample only for fun ;)
The main reason to make a .gih brush with more than 1 dimension is related to some nuances of the stains, for example, in some brushes is interesting to have a small random noise on the brushstroke borders, but each case is a case. To general proposals, the .gbr + paint dynamics is indicated but the .gih are for the specific usages or customized painting styles.
The Gih Dialog Box
The brush is not created to drawing or painting… only to make a practical example of 2 dimensions gih matrix, but I’ve made a sample only for fun ;)
 |
| A few samples with the .gih matrix brush example... only to have a picture ;-) |
Conclusions
I’ve been making .gih brushes since 2008… and its matrix is a thing very difficult to understand. I’ve studied this matrix many times in different periods… and is always a bit complex to remember how to use it effectively on painting issues. Then I thought to write this document, to make a big picture to help ourselves that is necessary some tutorials and practical methods to use this resource. In past, I was a bit convinced that doesn’t have a sense of the .gih brushes with more than 1 dimension… but was personally difficult to understand how to use the .gih brushes in digital painting in that moment. Common sense is that the .gbr + paint dynamics is sufficient to emulate the main aspects of the pictorial technique on digital painting... and is in great part correct... but also the .gih has an important role to emulate the specific cases of the personal styles and tasks.The main reason to make a .gih brush with more than 1 dimension is related to some nuances of the stains, for example, in some brushes is interesting to have a small random noise on the brushstroke borders, but each case is a case. To general proposals, the .gbr + paint dynamics is indicated but the .gih are for the specific usages or customized painting styles.
References
Video about Gimp Gih matrix - Dimensions versus AspectsThe Gih Dialog Box



Comments
Post a Comment
Comment